UPDATE: The Ministry of Infrastructure and the Environment stopped financing Climate Dialogue, at which point both PBL Netherlands Environmental Assessment Agency and the Royal Netherlands Meteorological Institute (KNMI) stopped their involvement in this project. The blog ClimateDialogue will remain online until 1 January 2016 and Marcel Crok will take on the responsibility for its continuation. Neither PBL nor KNMI will be responsible for any text written after 1 January 2015.
++++
According to the latest IPCC report, AR5, the influence of the sun on our climate since pre-industrial times, in terms of radiative forcing, is very small compared to the effect of greenhouse gases.
According to some more skeptical scientists such a small solar influence is counterintuitive. The Little Ice Age, the period roughly from 1350 to 1850, in which winters on the Northern Hemisphere could be severe and glaciers advanced, coincided with the so-called Maunder Minimum, a period of supposedly low solar activity. In their eyes, the sun therefore still is a serious candidate to also explain a substantial part of the warming since pre-industrial times.
Sunspot records since 1600 suggest there has been a considerable increase in solar activity in the 20th century leading to a Grand Solar Maximum or Modern Maximum. However recently these sunspot records have come under increasing scrutiny and newer reconstructions show a much ‘flatter’ sunspot history. This challenges the idea of a Modern Maximum.
The current solar cycle 24 is the lowest sunspot cycle in 100 years and the third in a trend of diminishing sunspot cycles. Solar physicists expect cycle 25 to be even smaller than Cycle 24 and expect the sun to move into a new minimum, comparable with the Dalton or even the Maunder Minimum. Studying such a minimum with modern instruments could potentially answer a lot of the questions surrounding the influence of the sun on our climate.
We are very pleased that no fewer than five (solar) scientists have agreed to participate in this exciting new Climate Dialogue: Mike Lockwood (UK), Nicola Scafetta (US), Jan-Erik Solheim (NO), José Vaquero (ES) and Ilya Usoskin (FI).
The introduction and guest posts can be read online below. For convenience we also provide pdf’s:
Introduction What will happen during a new Maunder Minimum
Guest blog Mike Lockwood
Guest blog Nicola Scafetta
Guest blog Jan-Erik Solheim
Guest blog Ilya Usoskin
Guest blog José Vaquero


Let’s start the dialogue with our first question: What is according to you the “best” solar reconstruction since 1600 (or even 1000) in terms of Total Solar Irradiance?
Lockwood in his guest blog uses an interesting two step approach to this question. First he uses the PMOD dataset to get an impression of how Total Solar Irradiance decreased in the recent “low” solar activity cycle 24. The difference with earlier cycles in the PMOD dataset is rather small (0.38 W/m2). See his figure 1:
In step 2 he correlates sunspots with TSI. In 1900 solar activity based on the sunspot record was similar as today. So TSI should be as well. See his figure 2:
Conclusion: if the correlation between sunspots and TSI (as determined in the PMOD period since 1979) is pretty good, then TSI must have been similar then and now. It also means TSI reconstructions since 1700 are rather flat.
Now this contrasts with the TSI reconstruction that Scafetta and Solheim prefer, the one of Hoyt and Schatten 1993 (in combination with the ACRIM dataset, in which Scafetta is involved). See e.g. Solheim’s figure 2A:
Now if we look at the sunspot record that Solheim shows in his figure 5, this agrees with Lockwood’s record showing similar levels in 1900:
This suggests the difference in the TSI reconstructions is mainly based on using PMOD or ACRIM. Is that correct? Does that explain all the differences between your TSI reconstructions?
These questions are first of all posed to Lockwood, Scafetta and Solheim, but Usoskin and Vaquero of course are more than welcome to weigh in.
With respect, it’s really not that simple. You are implicitly assuming instantaneous equilibration of at least the 0-700m oceans there. You maybe need to explicitly state why you are assuming that.
Activity over the last 60 years has been consistently higher than in the 60 years preceding the early 20th c. minimum. If there is a solar influence there will considerable lag due to thermal inertia of the oceans. Just comparing the current solar max to an earlier cycle is not sufficient to confirm or refute.
Please refer to my other post here showing the need to consider other factors in attempting to discern whether there is a solar influence.
Prof. Solheim shows a graph with the Ljungqvist reconstruction (figure 6 in his post) and states the following:
“Following Ljungqvist my conclusion is that the LYA NH extra-tropical temperature difference is more than one degree °C for a decadal average temperature compared with the last decade.”
The graph of Ljungqvist becomes more interesting when you add the decadal averages after the year 1999, which is the last point of the instrumental data in the original graph:
https://klimaatverandering.files.wordpress.com/2014/10/ljunqvist_reconstruction_gistemp_hadcrut_2013.png
The LIA NH extra-tropical temperature difference with the last decade increases to about 1.4 – 1.6 °C and the temperature difference of the MWP maximum with the last decade is about 0.5 – 0.7 °C.
I fail to see the correlation with the Ljungqvist reconstruction (and even more so with the last decade added) and sunspot numbers in the bottom panel in figure 5 of the post of Prof. Solheim. For instance the high number of sunspots around 1600 or 1750 and the low temperature in the NH extra tropics in that period? Would Prof. Solheim be so kind to explain this lack of correlation?
It is unrealistic to expect an instantaneous response to solar variation. Just the top ocean “mixed layer” has an enormous heat capacity. Also any change in SST will invoke the strongly negative Plank feedback, amongst others meaning SST will take tome to settle to a new dynamic equilibrium. The most simplistic way to model this kind of response is an exponential relaxation to equilibrium ( calculable by convolution with a suitable exponential decay ). This is in line with linearised IPCC thinking and the idea of a change in radiative forcing leading to a final change in surface temperature.
As an illustration, here is a response with a 5 year time-constant applied to Svalgaard’s modified SSN compared to hadSST3 global average SST.
http://climategrog.wordpress.com/?attachment_id=981
The scaling was arbitrarily chosen to align the two series. The 0.6 deg C offset is freely chosen since the reference period for the SST “anomaly” is equally arbitrary.
It is notable that the decadal variability in the two series only matches coincidentally in certain periods. There is a persistent phase drift showing that different periodicities dominate the two series on the decadal scale.
Peaks from the more reliable post-WWII data strongly suggests a decadal lunar influence in SST. This is explained in detail in the text. This is in accord with much of N. Scafetta’s work.
There is little convincing evidence of a circa 11 year signal in any climate data. Most such claims have relied on selective periods where the lunar signal in phase with SSN to arrive a spurious correlations.
There is fair similarity on the inter-decadal scale for most of the SST record, if the significant “bias corrections” applied by Hadley Centre are correct. However, there is a divergence that starts in the late 1980s which raises a question of whether there is a correlation.
A clue to this divergence is to be found in satellite measurements of the temperature of the lower stratosphere:
http://climategrog.wordpress.com/?attachment_id=902
The two step changes are clearly attributable to the two major eruptions. This step nature is now recognised by NCAR and AR5 but the implications for the lower climate are not followed through.
A cooling in the TLS data implies a change in energy budget at the tropopause. Simply put cooling in TLS accompanies warming of the lower climate system.
Both events left a clear, definitive change in the composition of the lower troposphere ( principally depletion of UV absorbing ozone ) and TLS. ERBE top of atmosphere energy budget data shows an additional 1.8 W/m2 of short-wave ( UV) energy entering the Earth climate system since Mt Pinatubo. Since the stratosphere shows cooling, this energy must end up in the lower climate.
The change after the earlier El Chichon event would seem to be comparable.
An extra 1.8 W/m2 due to a major stratospheric eruption is large enough and corresponds closely in timing to explain the recent divergence of SST and SSN.
There is no single driver of climate variability. In order that attribute of refute solar influence it is necessary to recognise other factors that are present, otherwise there will be either false attributions or spurious rejection.
Jan-Erik Solheim:
This is in agreement with what I presented earlier about TLS and ERBE TOA measurements. However, I think the current value for AOD is severely under-estimated.
Lacis et al 1992 ( see article ) made detailed physically based calculations and came up with an estimation of 33 for the scaling of AOD to W/m2. This later got reduced to 21 on the basis that it better matched GCM model output. This is symptomatic of weight given to GCMs. In Hansen et al, ten years later, they chose to rescale the data rather than question the model. The two authors were involved in both papers.
I used a study of ERBE data around Mt Pinatubo event to derive aerosol forcing and came very close to the original Lacis figure of 33.
http://climategrog.wordpress.com/?attachment_id=884
In which case ΔT=0.13°C becomes about 0.2°C
In this CD post we have two representatives of the consensus view (large CO2 influence on recent climate with little solar influence), two from the contrarian view (solar has been dominant), and one in the middle. This is not my field, so I am curious whether this is a representative sampling of expert views on this topic.
Here’s what the IPCC says about the total amount of radiative forcing in W/m2 contributed by human activity (mostly burning fossil fuels) from the years 1750-2005:
————————————————-
“The understanding of anthropogenic warming and cooling influences on climate has improved since the TAR, leading to very high confidence that the effect of human activities since 1750 has been a net positive forcing of +1.6 [+0.6 to +2.4] W m–2.”
————————————————-
So, according to the IPCC, the total amount of radiative forcing contributed by humans to the energy flux balance has been just 1.6 W/m2 during the 256 years between 1750 and 2005. The IPCC authors also wrote this about how climate change occurs:
————————————————
“Global climate is determined by the radiation balance of the planet (see FAQ 1.1). There are three fundamental ways the Earth’s radiation balance can change, thereby causing a climate change: (1) changing the incoming solar radiation (e.g., by changes in the Earth’s orbit or in the Sun itself), (2) changing the fraction of solar radiation that is reflected (this fraction is called the albedo – it can be changed, for example, by changes in cloud cover, small particles called aerosols or land cover), and (3) altering the longwave energy radiated back to space (e.g., by changes in greenhouse gas concentrations). In addition, local climate also depends on how heat is distributed by winds and ocean currents. All of these factors have played a role in past climate changes.”
————————————————
Of course, (3) is where the 1.6 W/m2 of anthropogenic RF comes into play. The changes in surface incident solar radiation (2) are elicited primarily by changes in clouds and aerosols (albedo). Simply put, more cloudiness and aerosol depth means less sunlight penetrates to the Earth’s surface, or dimming. Less cloudiness and aerosol depth means more sunlight reaches the Earth’s surface, called brightening.
There is a well documented record of global brightening and global dimming trends during the 20th century. And this record clearly shows a correlation with temperature, and a much, much stronger radiative forcing (W/m2) influence relative to the anthropogenic influence. During the 1980s to 2000s alone, albedo changes (brightening) contributed between 2.5 and 10 W/m2 of radiative forcing, which directly corresponds to the warming that took place during this period. This easily dwarfs the radiative forcing strength of the anthropogenic influence alleged by the IPCC (0.3 W/m2 per decade between 1951 and 2011).
Below are some of the many papers that document the global brightening and dimming trends of the 20th century, including the dimming that led to flat to cooler temperatures during the 1950s-1980s, and the brightening that led to the warmer temperatures in the 1980s, 1990s, and 2000s.
—————————————
ftp://bbso.njit.edu/pub/staff/pgoode/website/publications/Palle_etal_2005a_GRL.pdf
Traditionally the Earth’s reflectance has been assumed to be roughly constant, but large decadal variability, not reproduced by current climate models, has been reported lately from a variety of sources. There is a consistent picture among all data sets by which the Earth’s albedo has decreased over the 1985-2000 interval. The amplitude of this decrease ranges from 2-3 W/m2 to 6-7 W/m2 but any value inside these ranges is highly climatologically significant and implies major changes in the Earth’s radiation budget.
—————-
http://onlinelibrary.wiley.com/doi/10.1002/2014JD021877/abstract
Radiative forcing in both the short and long-wave lengths reaching the Earth’s surface accounted for more than 80% of the inter-annual variations in the mean yearly temperatures measured at Potsdam, Germany during the last 120 years [1893-2012]. Three-quarters of the increase in the long-wave flux was due to changes in the water content of the lower atmosphere; the remainder [25%] was attributed to increases in CO2 and other anthropogenic, radiatively active gases. Over the period radiative forcing in the short-wave flux [solar forcing] slightly exceeded [0.76 W/m2 per decade] that in the long wave [0.64 W/m2 per decade].
[The total long term radiative forcing for the Sun was 9.12 W/m2 for the 120-year period. The total long term radiative forcing from CO2 was 1.92 W/m2 for the 120-year period.]
—————-
http://journals.ametsoc.org/doi/abs/10.1175/JCLI-D-12-00482.1?journalCode=clim
Data from this summation method suggest that surface incident solar radiation increased at a rate of 6.6 W m−2/decade−1 (3.6%/ decade) from 1992 to 2002 (brightening) at selected sites.
—————-
http://www.sciencedirect.com/science/article/pii/S1352231014007456
Total global solar shortwave (G) irradiation and sunshine duration were recorded at nine Spanish stations located in the Iberian Peninsula. Averaged series (using the nine locations) showed a statistically significant decrease in annual G [global dimming] from 1950 to the mid 1980s (−1.7%dc−1) [-8.5 W/m2] together with a significant increase [global brightening] from the mid 1980s to 2011 (1.6%dc−1) [+8 W/m2].
—————–
http://onlinelibrary.wiley.com/doi/10.1029/2008JD011290/abstractThe decadal trend shown in the 5-year running mean indicates a period of rapid increase [solar radiation reaching the surface/brightening] starting in late 1930s and continuing to early 1950s with a change of 10 W m2. The dimming trend from the early 1950s to the late 1980s shows a decrease of 13 W m2. The subsequent increase starting in late 1980s is about 10 W m 2 by 2005. These changes are not confined to a small number of stations in western Europe, but shared by more than 400 other sites where global irradiance has been continuously observed for more than 40 years.
—————
http://onlinelibrary.wiley.com/doi/10.1029/2010JD015396/abstract
We find distinct patterns of dimming and brightening in the aerosol optical depth and thus clear-sky downward surface shortwave radiation (SSR) in all analyzed subregions. The strongest brightening between 1973 and 1998 under clear-sky conditions is found in mid-Europe (+3.4 W m−2 per decade [8.5 W m−2 total], in line with observations).
——————
http://www.sciencemag.org/content/308/5723/850.abstract
Long-term variations in solar radiation at Earth’s surface (S) can affect our climate, the hydrological cycle, plant photosynthesis, and solar power. We observed an overall increase in S [solar radiation] from 1983 to 2001 at a rate of 0.16 watts per square meter (0.10%) per year [3.04 W/m-2 total].
——————
http://www.atmos-chem-phys.net/13/8505/2013/acp-13-8505-2013.html
[T]here has been a global net decrease [of 3.6%] in 340 nm cloud plus aerosol reflectivity [which has led to] an increase of 2.7 W m−2 of solar energy reaching the Earth’s surface and an increase of 1.4% or 2.3 W m−2 absorbed by the surface [between 1979 and 2011].
——————
http://journals.ametsoc.org/doi/pdf/10.1175/BAMS-D-11-00074.1
Literature estimates for the overall SSR decline during dimming (1950s to 1980] range from 3 to 9 W m−2, and from 1 to 4 W m−2 for the partial recovery during subsequent brightening [1980s to 2000] (Stanhill and Moreshet 1992; Liepert et al. 1994; Abakumova et al. 1996; Gilgen et al. 1998; Stanhill and Cohen 2001; Alpert et al. 2005; Kvalevag and Myhre 2007; Kim and Ramanathan 2008; Wild 2009).
——————
http://onlinelibrary.wiley.com/doi/10.1002/joc.4107/abstract
The annual sunshine duration mean time series shows a decrease from the early 1960s to the late 1970s [in Iran], in line with the widespread dimming of surface solar radiation observed during this period. By the early 1980s, there is an increase in sunshine through the end of the 20th century, aligning with a well-known and well-documented brightening period.
What effect does the precession of the earth have on the earth’s reception of solar energy? I believe the earth is currently in a more vertical position than it was during the 1700s.
Expected temperature decrease in the coming Maunder Minimum (an update)
Since I wrote my first blog, new TSI reconstructions have been published by Velasco Herrera et al. (2015). In this paper they present a new method, which they call Least Squares Support Vector Machines, to estimate the TSI index from year 1000 to 2100 AD. They use the PMOD and ACCRIM composites for calibration, and they have generously given me their data sets to investigate.
Below are the two estimates, which I have compared with the Central England temperature measurements since 1659:
In both cases the Central England temperature (CET) is drawn in black, while the TSI estimates are in red. CET follows both quite well after 1850, but V-ACC (TSI estimate based on ACCRIM) correspond better in the minimum around 1970. The big difference is before 1850. Here CET follows V-ACC quite well, while it is systematically higher than the V-PMOD estimates.
Based on this comparison, I conclude that the CET, which is a good proxy for the global temperature, follows V-ACC better, and I select this as the better choice for estimating the global temperature change for the coming minimum.
The two reconstructions give slightly different dates and length for the coming minimum: TSI(PMOD) has an estimated minimum 2004-2075 with a TSI-reduction of 0.09 W/m2. The estimate based on ACCRIM has minimum 2002-2063 and a TSI-reduction of 0.18 W/m2.
To convert the TSI to global temperature, I use the results just published by Harde (2014). He uses an advanced two-layer climate model to calculate the influence of an increasing CO2-consentration and a varying solar activity on global warming. His simulations including an increased solar activity the last century give a CO2 initiated warming of 0.2°C and a solar influence of 0.54°C during this period. The CO2 climate sensitivity (for doubling) becomes 0.6°C, and the solar sensitivity is 1.15°C for 0.1% TSI(V-PMOD) or 0.9°C for 0.1% TSI (V-ACC) increase.
For the two TSI reconstructions and a CO2 increase of 2 ppm per year, I have calculated that the global temperature change in the coming minimum will be -0.23°C based on TSI(V-PMOD) and -0.80°C based on the TSI(V-ACC) estimates.
Since the Central England Temperature followed TSI(V-ACC) best I conclude that a GST estimate based on TSI(V-ACC), giving -0.8 °C relative last decade, is most likely for the coming minimum..
References:
H. Harde, Advanced Two-Layer Climate Model for the Assessment of Global Warming by CO2, Open Journal of Atmospheric and Climate Change, ISSN(print): 2374-3794 ISSN(Online): 2374-3808, 2014 In Press
V.M. Velasco Herrera, B. Mendoza and G. Velasco Herrera, Reconstruction and prediction of the total solar irradiance: From the Medieval Warm Period to the 21st Century, New Astronomy, 24, 221-244, 2015
It is important to include all the relevant facts and arguments in a discussion like this. Much of the work on solar cycles presented here has been critizised in a collection of replications by Benestad (2014): Replication of a number of contrarian climate change studies. figshare. http://dx.doi.org/10.6084/m9.figshare.951971 and the discussion paper ‘Agnotology: learning from mistakes’: http://www.earth-syst-dynam-discuss.net/4/451/2013/esdd-4-451-2013.html.
When scrutinised, we find that the so-called cycles in observed climate can have any cause. They may not even be robust, but may be part of a transient behaviour in a chaotic system. However, there are also some weak ‘solar signal’ (variations that seem synchronised with sunspots) in the climate data, and the most intriguing feature seems to be around the North Atlantic, as Lockwood observes (http://iopscience.iop.org/1748-9326/8/3/035049/article). Apart from that, there is little evidence suggesting a strong connection between the current global warming and solar activity – there has been little long-term change in the sun since the 1950s, except for the most recent weak solar cycle (http://goo.gl/8Dtkrt).
There is a European project that looks into questions like these: COST-TOSCA. More information about this can be found on http://lpc2e.cnrs-orleans.fr/~ddwit/TOSCA/TOSCA/Home.html.
Rasmus Benestad
Dr Usoskin states:
The issue is that no one knows when the new Grand Minimum occurs and no one really knows what would happen then. I call such extended minima of suppressed solar activity Grand Minima, since the Maunder Minimum (lasting from 1645 till about 1700 or 1712) is only one of those. Later minima, such as the Dalton Minimum (ca. 1800 AD) and modern (ca. 1900 AD) ones were not really Grand Minima, in neither depth or duration.
There is new science which makes it very easy to predict any solar cycle/grand maximum/grand minimum in the future that is now recognized by science. This knowledge has been around since 2008 and can be utilized to hindcast the Holocene with very good accuracy. The new method is published in a peer reviewed journal(Sharp 2013) and is also backed up by another paper by McCracken et al(2014).
The new knowledge remedies the errors made by Landscheidt and Charvàtovà and can be downloaded for free at:
http://www.scirp.org/journal/PaperInformation.aspx?paperID=36513&#reference
and the McCracken paper is available at:
http://link.springer.com/article/10.1007/s11207-014-0510-1
Once the theory is understood grand minima can be recognized by the dynamo disruption occurring rather than the depth of the grand minima involved. Grand minima such as the Dalton observe this dynamo disruption and cannot be ignored.
Reply to Jos Hagelaars’ comment:
I fail to see the correlation with the Ljungqvist reconstruction (and even more so with the last decade added) and sunspot numbers in the bottom panel in figure 5 of the post of Prof. Solheim. For instance the high number of sunspots around 1600 or 1750 and the low temperature in the NH extra tropics in that period? Would Prof. Solheim be so kind to explain this lack of correlation?
I agree there is a jump in the Northern hemisphere temperature from the 1980ies to the period after 2000. It will be interesting to see how trees react to this jump, since most of the changes have been related to milder winters and warmer spring and fall in the North. It is always a danger to combine proxy temperatures from trees, which may not respond fast, to instrument temperatures. The graph below shows the difference between the North, Equatorial and South in satellite tropospheric temperature, and we find a large temperature jump in the North, a small in the South, and none in Equator region:
Temperature observations by satellites as interpreted by Drs Roy Spencer and John Christy, at University of Alabama (graph from climate4you.com)
When it comes to the lack of correlation around 1600 or 1750, it may be that the proxies are too slow to react to these short periods of increased solar activity. If we assume that the sunspot no is proportional to the heat the Earth receives, we have to compare areas under the average sunspot curve, which is much larger in the period 1780-2000. If we instead look at the TSI reconstruction (figure 2 in my second blog), we see quite nice correlation with CET – also around 1750.
Reply to Greg Goodman:
Thanks – a very helpful comment. The sudden jumps in temperature need to be explained. But can you explain why the jumps are bigger in the Northern Hemisphere temperature records?
Greg Goodman, it is unrealistic to expect surface temperature anomaly to respond quickly and it is also unrealistic to expect region temperature anomaly to accurately represent energy anomaly.
RSS provides TLT temperatures in absolute values via Climate Explorer which allows estimation of energy anomaly using Stefan-Boltzmann. Not ideal by any stretch, but a better way to at least double check relationships.
https://lh3.googleusercontent.com/-MciM025vRzo/VE56_E0r1hI/AAAAAAAALqs/3_C4GBbI3Sg/w761-h507-no/RSS%2BEnergy%2Banomaly.png
That compares the estimated energy anomaly for the regions using in the UAH example. That is more realistic considering the differences in land to water ratio plus absolute temperature. If you want a more rapid response, there are stratospheric data sets which are also available in absolute values. As a general rule, only the tropical surface band is useful for direct comparison to solar and even that has more than enough noise to challenge most folks thanks to delays of roughly ~27 and ~96 months associated with ocean surface and bulk layer mixing (QBO and ENSO mainly). Since solar and volcanic are likely interrelated, before long things can get a bit complicated.
The plots that Jan-Erik Solheim shows between CET [Central England Temperature] and TSI reconstructions are really interesting but must now be evaluated with proper statistical testing against the null hypothesis. Agreements of the kind he presents, and indeed seemingly even closer ones, do often happen by chance and it is vital to test if there is any significance in the similarities or not. I will not here pre-judge what I think those tests are likely show, but they must be done.
I have carried out some statistical significance testing of winter Central England temperature (CET) against solar activity and did find a weak signal there that was indeed statistically robust in that there were more cold winters when solar activity was low [Lockwood et al., 2010]. (Winter here means December-January-February (DJF) averages).
I did also find a tendency for more hot summers when solar activity was low, which I was very excited about because it would have been consistent with our interpretation of the winter data in terms of enhanced jet stream blocking in the eastern Atlantic when solar activity is low. However, this summer relation failed the statistical tests, yielding a very high probability that it was just a chance occurrence. Thus there is no evidence that there is a corresponding effect on summer blocking events. This is, in fact, not surprising because the equator-to-pole temperature gradient in the lower stratosphere/upper thermosphere which drives the jet stream is very much weaker in summer than in winter and modelling of the solar activity effect strongly suggests it is a predominantly a winter phenomenon.
But the statement I would take issue with immediately is “I conclude that the CET, which is a good proxy for the global temperature, ….”. This is a major assumption that is not supported by the data. The figure below shows global regression maps by Lean [2010].
These are maps of the detected surface temperature responses in data for 1980-2008 to input data series of El-Niño (ENSO), volcanic forcing, solar variability, and anthropogenic forcing. The fit residuals at each point (not shown) are attributed to natural internal variability. This is multiple regression analysis, exactly like that shown in figure 3 of my blog except that the regression has been carried out for the temperature in each pixel of the map, not on the global mean temperature.
To avoid the relative scaling of the plots reflecting the relative radiative forcings of each input, each response map has been scaled to the response for a known event: these are (from top to bottom): the ‘‘super El Niño’’ event of 1998, the Pinatubo volcanic eruption, solar cycle 23 and the net anthropogenic forcing over the period 1980–2006. These are very similar in form to the maps of the regression coefficients presented by Lean and Rind (2008) that did use the radiative forcings. Note that these are not proper detection-attribution studies because the internal variability has not been modelled and so it is possible noise features have been “over-fitted”.
As discussed in my blog, we know that the effect of over-fitting was small in the studies of the global mean temperature but it remains a potential factor in these regression maps. However, looking at the responses to El-Niño, volcanic and anthropogenic forcing, the results are explicable and consistent with climate modelling suggesting over-fitting is not an issue here either. Looking at the top panel, as expected, the El-Niño response is dominated by the equatorial Pacific, but with significant (so-called) “teleconnection” responses elsewhere, particularly North America. The cooling effect of the volcanic forcing is seen in the second panel to be global, but there are some regions where the opposite response is seen.
Moving to the bottom panel the response to anthropogenic forcing is very much as predicted by models, with the greatest response over land and hence in the land-dominated northern hemisphere. The response is the expected temperature rise at most locations over the globe but there are some small regions where the opposite is seen.
Lastly the third panel shows the response to solar activity. It can be seen to be primarily a Eurasian phenomenon (under the northern hemisphere jet stream after it has hit land after crossing the Atlantic), and central England lies at the western end, but inside, this region. Note that our studies with the ERA-40 re-analysis data during the satellite era reveal that low solar activity gives colder winters in Eurasia but this is accompanied by warmer winters in Greenland/Arctic Canada region [Woollings et al, 2010]: this is not seen in the figure because there were insufficient data in this region. This highlights how easy it is for biases to be introduced by regional and seasonal effects because the Greenland/Arctic Canada changes in the Woollings et al. [2010] study largely counterbalance the Eurasian effect, but that counterbalancing is missing in the dataset used in the Lean [2010] study because of the missing Arctic data.
The key point is that CET is certainly not representative of a global response to solar forcing. This is precisely the points about the crucial difference between regional and global mean responses that I was making in points (1) and (2) of my blog.
The regionality of the response to solar forcing seen in the figure is extremely significant because as we go back in time our surface temperature observations become more and more weighted to precisely the Eurasion region where we find this response (which is, in fact, largely a winter response). Care must be taken with even paleoclimate data to ensure that they are taken from sites which avoid a bias being introduced by this regionality.
References
Lockwood M, Harrison RG, Woollings T, Solanki SK (2010) Are cold winters in Europe associated with low solar activity? Environ Res Lett 5:024001. doi:10.1088/1748-9326/5/2/024001
Lean J (2010) Cycles and trends in solar irradiance and climate. Wiley Interdiscip Rev Clim Change 1(1):111–122. doi:10.1002/wcc.018
Lean JL, Rind DH (2008) How natural and anthropogenic influences alter global and regional surface temperatures: 1889 to 2006. Geophys Res Lett 35:L1870. doi:10.1029/2008GL034864
Woollings T, Lockwood M, Masato G, Bell C, Gray L (2010) Enhanced signature of solar variability in Eurasian winter climate. Geophys Res Lett 37:L20805. doi:10.1029/2010GL044601
Very interesting perspective.(Responding to Ilya Usokin). More solar variation but also lots of “randomness”. If this randomness can be taken as the result of a very complex system of imputs rather than an excuse to go play golf, we have a lot of work to do.
Jose Vaquero: If you believe the “little ice age” was caused by internal variability,do you believe a true ice age can be caused by internal variability? Not a stadial, the five to ten million year affairs with wide wings.
Unfortunately, I see no real way to define “the best” TSI reconstruction in the past. The problem is that we have no independent way to “validate” such a reconstruction outside the training period.
Let me explain. A normal way of reconstructing a quantity X from a proxy data Y, using a mathematical/statistical/empirical relation in the absence of a full physical model relating the reconstructed quantity X and the proxy Y, consists of several steps:
(1) selection of a “training” period when both X and Y are known with good accuracy;
(2) building a model (let us call it a regression) relating Y to X and optimizing it;
(3) selecting a “validation” period when both X and Y are known, but were NOT used to build the regression; it is crucial that data from the “validation” period are not used in the training of regression.
(4) for the “validation” period, values of X’, the reconstructed from Y values, are compared with the real values of X to validate the regression.
Ideally, “validation” period should be at least as long as the “training” period or better longer. However, this procedure cannot be done for TSI reconstructions for the obvious reason. The measured TSI series (X) is too short to split it in parts. Moreover, until the 2000s it was totally dominated by the 11-yr cycle without a secular change. Only after 2006 there is a hint for the secular change but it is too short to make a reliable regression. Thus, any extrapolation of the regression between TSI and a proxy is not “validated” in the strict sense, and may fail, and what is worst, this failure cannot be controlled.
Another problem is that the centennial variability cannot be in any way controlled since the “training” period is too short for that.
Figure 1. A regression between group sunspot numbers (GSN) and 10Be concentration in an ice core for the period 1700-2010. Small red dots depict the annual values, while big yellow dots – the 11-yr averaged values.
Different regressions are shown: yellow line corresponds to the regression built using 11-yr averaged data for the entire period, while the green line – annual values for the period 1950-2010 [Modified after Usoskin & Kovaltsov, 2004]. One can see that a regression built using annual values for 1950-2010 leads to wrong results when used on a centennial time scale.
We have made a clear case of such a failure using 10Be data (Usoskin & Kovaltsov, Solar Phys., 224, 37, 2004) – see the plot above. Let us assume we have annual data of 10Be and GSN only for the period 1950-2010 (as shown by the green oval), and we build a regression for that period (as shown by the blue line). Then we happily extrapolate the regression (blue line) backwards down to 1700 AD, and… get wrong results. Fortunately, we do have both 10Be and GSN data since 1700 to validate the relation. It is obvious that a regression built for the period 1950-2010 doe NOT reproduce the centennial trend adequately. The same situation may happen for TSI reconstruction but since we do not have a mean to validated TSI values in the past, we do not know that.
All this is explained simply by the strong non-linearity of the relation which make the regression to depend on time scale, averaging, etc.
In such a situation, there is no way to select a “best” reconstruction.
In this sense, the most favorable is a reconstruction by the German group (Krivova, Solanki) who use not a regression but a physics-based model. Still it has one parameter whose value is found by fitting the data, but at least it intrinsically includes possible non-linearities.
And I don’t believe that solar activity and hence TSI can be predicted in the future in a deterministic sense. Only in the probabilistic one.
Comments to Mike Lockwood :
I agree that CET is not global, but still it may be one of the best series to investigate long time changes. In particular since it covers a significant part of the Maunder Minimum, which is a topic in this discussion
A reason for using data from one location is the better control of the data. The global temperature is a composite of many thousand recordings, and the number of stations and weighting scheme changes with time. Observations, done with care during centuries, from a well preserved site, may be a better for detecting long time changes as explained by Butler (1994) for Armagh Observatory. He finds a good correlation between Armagh and NH temperatures. However, the Armagh series reach back only to 1844.
The global regression maps for Pinatuba shows the same global cooling as calculated by Greg Goodman (2014-10-18) of 0.2 °C
Reference
C. J. Butler, Solar Physics, 152, 35, 1994
Question to Mike Lockwood:
I find your multiple regressions quite impressive, but which of the parameters used in your Fig 3 explains the obvious correlation between cloud cover and global temperature as shown below?
Comment to Mike Lockwood and Ilya Usoskin:
The CET data set covers 355 years. To investigate the relations between CET and TSI I have split the data set in two parts, each 177 yrs long, and compared with the two TSI reconstructions by Velasco Hererra et al. as shown in my previous comment.
A: Central England Temperature versus TSI calibrated with PMOD:
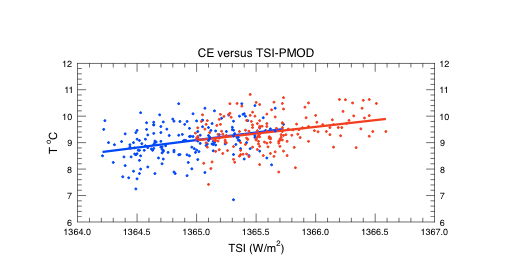
The first 177 yrs are shown with blue dots, and the last with red dots. I find the same slope for the two parts. A CET average temperature of 9.4 °C can be estimated for their grand minimum period 2004-75 based on the linear relation based on all data 1659-2013.
B. Central England Temperature versus TSI calibrated with ACCRIM.
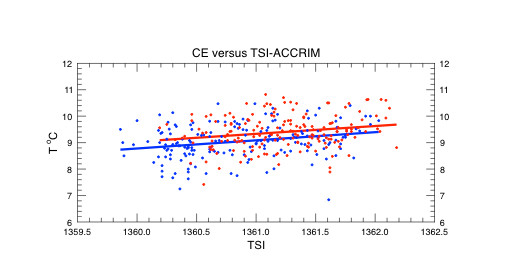
With the TSI-ACCRIM calibration the temperature gradient is the same for the two subsets, but the last 177 yrs (red) is shifted up 0.1 °C. Estimated CET average temperature for the grand minimum period 2002-2063 based on the relation 1835-2013 is 9.2 °C.
Temperature change to the next minimum
The average CET temperature 1994-2013 is 10.2 °C. Temperature decrease based on TSI with PMOD will be 0.8 °C for the period 2004-75. Based on TSI-ACCRIM it will be 1.0 °C for the period 2002-63. Since the temperature gradient from Equator to Pole also changes with TSI (Soon and Legates, 2013), the change in global temperature will probably be less.
Reference
W. Soon and D. L. Legates, Solar irradiance modulation of Equator-to-Pole (Arctic) temperature gradients: Empirical evidence for climate variation on multi-decadal timescales, Journal of Atmospheric and Solar-Terrestrial Physics, 93, 45-56, 2013
The estimated cooling – already here?
One may wonder if the cooling already has started as indicated by the TSI drop
Since most of the heat goes into the oceans, it is interesting to notice that the average temperature 0-800m in the North Atlantic along 59N parallel has decreased 0.7 °C from the peak in 2006/2007, and it is still decreasing.
Dear colleagues,
My opinions are very close to the exposed ideas by Mike Lockwood and Ilya Usoskin.
I also think that we have a way to select a “best” reconstruction and, in any case, we would choose the reconstructions made using a physics-based model. A similar situation occurs with respect to the prediction of the solar activity (and TSI). The deterministic models fails and we can only find probabilistic solutions (see , for example, Solanki and Krivova, 2011).
Solanki, SK; Krivova, NA (2011) Analyzing Solar Cycles, Science 334, Issue 6058, p. 916.
Reply to gymnosperm:
If you believe the “little ice age” was caused by internal variability, do you believe a true ice age can be caused by internal variability? Not a stadial, the five to ten million year affairs with wide wings.
I wrote that my results suggest that Medieval Climate Anomaly (Diaz et al., 2011) was driven by the internal variability of the coupled ocean-atmosphere system, with the solar activity playing a minor role in this climatic episode. Of course, the origin of a “true ice age” is not our Sun but a combination of elements of the Earth System, including a set of cyclic variations in the Earth’s orbit around the Sun (Milankovitch cycles).
HF Diaz, RM Trigo, MK Hughes, ME Mann, E Xoplaki, and D Barriopedro (2011) Spatial and Temporal Characteristics of Climate in Medieval Times Revisited. Bull. Amer. Meteor. Soc. 92, 1487–1500.
I found the various posts quite interesting.
Marcel Crok asked about the “best” solar reconstruction since 1600 (or even 1000) in terms of Total Solar Irradiance (TSI). I will try to respond in various ways because unfortunately this question cannot be unanswered. There is a need of a detailed discussion.
All available TSI records are satellite measurements and they start in 1978. See the available TSI records at
http://acrim.com/
These records were combined to form composites. Two of the most common TSI composite were proposed by ACRIM and PMOD: see them at:
http://acrim.com/TSI%20Monitoring.htm
As the reader can realize, even the TSI composites are ambiguous: the ACRIM one shows an increase from 1980 to 2000 and a decrease afterward and the PMOD composite, which is the one also showed by Marcel Crok in his first figure, shows a multidecadal decadal decreasing patter.
It is important to remind that while the ACRIM composite uses the TSI measurements as published by the experimental teams, the PMOD composite uses altered records under a set of assumptions first proposed by Frohlich and Lean in 1998. The above reported ACRIM web-site explains in details the experimental issues.
In any case, one of our recent publications
Scafetta, N., and R. C. Willson, 2014. ACRIM total solar irradiance satellite composite validation versus TSI proxy models. Astrophysics and Space Science 350(2), 421-442.
http://link.springer.com/article/10.1007%2Fs10509-013-1775-9
has likely fully demonstrated that Frohlich’s assumptions are questionable and self-contradictory. Thus, in my opinion, the ACRIM TSI composite is closer to the truth. The sun should have experienced a secular maximum around 2000 contributing the global warming observed from ~1970 to ~2000. Since 2000 the solar activity has gradually decreased. In our paper we have also proposed a tentative prediction for the next decade in Figure 15.
I hope that the scientific community will fully understand the issues regarding the ACRIM and PMOD controversy. In my opinion, too many people have blindly believed PMOD without professionally checking the claims. Hopefully, our recent publication will clarify the issue. In fact, understanding solar activity during the last decades is necessary to understand the mechanisms driving the multidecadal and secular dynamics of solar activity.
This brings us to the issue regarding the secular and millennial solar patterns asked by Marcel Crok.
This issue is complicated by the fact that no TSI direct measurements exist before 1978. All TSI secular and millennial reconstructions are hypothetical models that are not even based on physical laws. They are proxy models! That is, they are based on hypothetical and unchecked relations among several solar related records.
A typical example of how easy a proxy model can be proposed and how physically misleading it can be has been suggested by Lockwood in his figure 2. There the sunspot record is used as a “proxy” for TSI to which it would be linearly and positively correlated in its smoothed curve. Using this proxy model Lockwood argued that since 1700 the TSI has been 6 times at the current value simply because this is what that is observed in the used smoothed curve of the sunspot number record. The argument is, of course, very hypothetical and rudimentary. Indeed, it is unphysical.
In fact, there are no robust physical evidences suggesting that the sunspot number record can be used to reconstruct TSI in the way Lockwood proposed. What is clearly known from physics is that sunspots reduce TSI emission: therefore, they contribute “negatively” to TSI variation. The physical reason why there appears to be a positive approximate correlation between TSI and the sunspot record is because solar faculae, that is, the bright spots also appear in grand number and extension during the sunspot maxima and their brightness usually, but not always, overcomes the darkness of the sunspots. Moreover, TSI is not modulated by sunspot and faculae alone. There is also the background radiation from the quite zone that is usually assumed to be “constant” without any solid physical evidence for it. Thus, it is evident that without knowing the dynamics of the faculae and of the background solar radiation any TSI proxy model based only on the sunspot number record is likely misleading.
If since 1978 TSI did what the ACRIM TSI composite shows, the physical and empirical evidences are that there exists a very complex non-linear relation between sunspot, faculae and background radiation. TSI cannot be reconstructed by using simple linear proxy models and even less by using the sunspot number record alone.
In figure 1A:
Scafetta N., and R. C. Willson, 2013. Planetary harmonics in the historical Hungarian aurora record (1523–1960). Planetary and Space Science 78, 38-44.
http://www.sciencedirect.com/science/article/pii/S0032063313000081
the sunspot number and a record of aurora observations since 1600 was compared. Although the two records are in general correlated, we also noted some significant discrepancy. Sometime, the two records have shifted patterns. For example, there appears to be a peak in the aurora record around 1940s while the sunspot record peaked around 1960. The issue is important because in the 1940s there was a maximum in the global surface temperature record. Thus, if one believes in the sunspot number record no correlation emerges between solar activity and global temperature. On the contrary, if the aurora record better mirrors solar activity and the TSI variation, then a good solar-climate correlation is observed.
Indeed, one way to test a TSI model is to see how well it may match with both the solar records and the temperature records available for the past. Several examples are shown in this recent paper of mines:
Scafetta N., 2014. Global temperatures and sunspot numbers. Are they related? Yes, but non linearly. A reply to Gil-Alana et al. (2014). Physica A 413, 329–342.
http://www.sciencedirect.com/science/article/pii/S0378437114005226
These examples, as reproduced in my figures above, clearly suggest a strong solar-climate link once specifics proxy models are used. The correlation appears poorer when other reconstructions are used.
To better address the issue there is a need to develop new solar proxy models that can at least include some physical properties of the dynamic of solar variation at the decadal to millennial scales. There is a need to understand what is physically causing this variability.
In a number of papers that I have published recently, the proposed theory is that solar activity is partially modulated by gravitational and electromagnetic forcings caused by the planets. Because the planets are moving harmonically around the sun, the sun is forced by harmonic forcings that drive harmonic variations in solar activity. Of course, also in this case, evidently expected physical non-linearities make the patterns a little bit more chaotic. However, we and other scientists have produced a number of papers where the evidences for a planetary modulation of solar activity seems overwhelming. For example:
Scafetta, N., 2014. The complex planetary synchronization structure of the solar system. In the Special Issue “Pattern in solar variability, their planetary origin and terrestrial impacts”, Eds: N.-A. Mörner, R. Tattersall, and J.-E. Solheim. Pattern Recognition in Physics 2, 1-19.
http://www.pattern-recogn-phys.net/2/1/2014/prp-2-1-2014.html
Scafetta, N., and R. C. Willson, 2013. Multi-scale comparative spectral analysis of satellite total solar irradiance measurements from 2003 to 2013 reveals a non-linear planetary modulation of solar activity depending on the 11-year solar cycle. In the Special Issue “Pattern in solar variability, their planetary origin and terrestrial impacts”, Eds: N.-A. Mörner, R. Tattersall, and J.-E. Solheim. Pattern Recognition in Physics 1, 123-133.
http://www.pattern-recogn-phys.net/1/123/2013/prp-1-123-2013.html
Scafetta N., and R. C. Willson, 2013. Empirical evidences for a planetary modulation of total solar irradiance and the TSI signature of the 1.09-year Earth-Jupiter conjunction cycle. Astrophysics and Space Science 348(1), 25-39.
http://link.springer.com/article/10.1007%2Fs10509-013-1558-3
Scafetta N., 2012. Does the Sun work as a nuclear fusion amplifier of planetary tidal forcing? A proposal for a physical mechanism based on the mass-luminosity relation. Journal of Atmospheric and Solar-Terrestrial Physics 81-82, 27-40.
http://www.sciencedirect.com/science/article/pii/S1364682612001034
Scafetta N., 2012. Multi-scale harmonic model for solar and climate cyclical variation throughout the Holocene based on Jupiter-Saturn tidal frequencies plus the 11-year solar dynamo cycle. Journal of Atmospheric and Solar-Terrestrial Physics 80, 296-311.
http://www.sciencedirect.com/science/article/pii/S1364682612000648
Scafetta N., 2010. Empirical evidence for a celestial origin of the climate oscillations and its implications. Journal of Atmospheric and Solar-Terrestrial Physics 72, 951-970.
http://www.sciencedirect.com/science/article/pii/S1364682610001495
In particular I would like to stress this last paper that summarizes and extends some of the findings of the previous ones and responds to the sole critiques until now proposed in the scientific literature:
Scafetta, N., 2014. Discussion on the spectral coherence between planetary, solar and climate oscillations: a reply to some critiques. Astrophysics and Space Science 354, 275-299.
http://link.springer.com/article/10.1007%2Fs10509-014-2111-8
The evidence collected until now is that to properly understand solar dynamics one needs to fully understand how solar activity works and how the sun is linked to the dynamics of the entire solar system. Proxy models based on planetary harmonics have been the only ones that have been showed to approximately hindcast both solar records and climate records throughout the Holocene until now. So, I think that future research will have to focus on these emerging issues and develop them.
Right now, to answer Marcel Crok’s question I would say that nobody knows the right answer. However, numerous evidences suggest that the TSI proxy models proposed by Lean, Solanki, Lockwood and others are unsatisfactory because purely based on proxy associations without attempting to understand the underlaying physics of why solar activity varies on a decadal to millennial scales. If the ACRIM TSI composite is right, those proxy models are surely wrong because they better fit the PMOD composite, although in some contradictory way as explained in our paper (Scafetta and Willson, 2014). The TSI model proposed by Hoyt and Schatten is old but it has good correlation with some climate records. Preliminary solar models based on planetary harmonics has been proposed and they seem promising, as shown in my figures above. In my papers an interested reader can find references to many other works from other authors recently published on this topic.
Now I would like to briefly answer a comment from Benestad made below on 2014-10-21 09:36:40. Here Benestad claims that “Much of the work on solar cycles presented here has been critizised in a collection of replications by Benestad (2014): Replication of a number of contrarian climate change studies. figshare. http://dx.doi.org/10.6084/m9.figshare.951971 and the discussion paper ‘Agnotology: learning from mistakes’:….”
Benestad’s claims are quite curious. Apparently Benestad ignores that his own referenced paper has been “rejected” for publication. On the web-site of the journal it is written: “This discussion paper has been under review for the journal Earth System Dynamics (ESD). A final paper in ESD is not foreseen.”
In fact, several authors have pointed out severe mathematical and physical errors in his paper. See here
http://www.earth-syst-dynam-discuss.net/4/451/2013/esdd-4-451-2013-discussion.html
In particular see my own extended comment here:
http://www.earth-syst-dynam-discuss.net/4/C312/2013/esdd-4-C312-2013.pdf
Section 3 of
Scafetta N., 2013. Discussion on common errors in analyzing sea level accelerations, solar trends and global warming. Pattern Recognition in Physics, 1, 37–57.
http://www.pattern-recogn-phys.net/1/37/2013/prp-1-37-2013.html
explains in details other math errors made by Benestad in another publication with Schmidt in 2009.